In the world of data, Biostatistics regression models are powerful tools for uncovering relationships between variables and making predictions. Although linear regression facilitates the prediction of continuous outcomes, it is ineffective when the target variable is categorical. That's where binary logistic regression steps in.
Binary logistic regression is a statistical technique used to model the relationship between one or more independent variables and a binary outcome—which means the dependent variable has only two possible values, such as “yes” or “no”, “success” or “failure”, or “0” and “1”.
Let’s dive into binary logistic regression: how it works, and why it’s indispensable in data-driven decision making.
Understanding Binary Logistic Regression
Binary logistic regression is part of the family of generalized linear models (GLMs). This method is used when the dependent variable is binary, and the goal is to estimate the probability of a specific event occurring based on one or more predictor variables.
For example: let’s say you want to predict whether a patient has a disease (1) or not (0) based on their age, cholesterol levels, and blood pressure. Here, the outcome variable is binary, and binary logistic regression can help model this relationship.
The logistic regression model predicts the probability (p) of the event occurring. However, instead of predicting p directly (which must be between 0 and 1), the model predicts the log-odds (also called the logit) of the event:
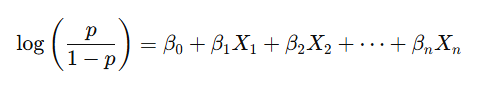
- p: Probability of the event (e.g., disease = yes).
- X₁, X₂, ..., Xₙ: Predictor variables.
- β₀: Intercept.
- β₁, β₂, ..., βₙ: Coefficients for each predictor.
By applying the inverse logit function, the log-odds can be transformed back into probabilities.
Why Not Use Linear Regression?
It might seem intuitive to use linear regression for binary outcomes, However, the approach possesses significant errors:
- Predicted Values Out of Bounds: Linear regression can predict values less than 0 or greater than 1, which don’t make sense when modeling probabilities.
- Non-Constant Error Variance (Heteroscedasticity): The variance of residuals in binary outcomes isn’t constant, violating one of linear regression’s core assumptions.
- Non-linearity in Probabilities: Binary outcomes often have a non-linear relationship with predictors—something linear regression doesn’t handle well.
Binary logistic regression overcomes these limitations by modeling the log-odds of the outcome and ensuring predictions stay within the 0–1 range.
Key Concepts in Binary Logistic Regression
1. Odds and Log-Odds
- Odds: The ratio of the probability that an event occurs to the probability that it doesn’t. For example, if the probability of success is 0.8, the odds are 0.8 / 0.2 = 4.
- Log-Odds: The natural logarithm of the odds. Logistic regression estimates these log-odds linearly.
2. Coefficients and Interpretation
The coefficients in a logistic regression model can be interpreted as follows:
- A positive coefficient increases the log-odds of the outcome.
- A negative coefficient decreases the log-odds.
Exponentiating a coefficient (eβ) gives the odds ratio, which tells us how the odds change with a one-unit increase in the predictor.
3. Model Fitting
Fitting a logistic regression model involves finding the coefficients (β) that maximize the likelihood of observing the given data. This is done through a method called Maximum Likelihood Estimation (MLE).
When and Why You Need Binary Logistic Regression
Binary logistic regression is indispensable in a variety of fields where binary outcomes are common. Here’s why:
Medical and Healthcare Research
Doctors and researchers use logistic regression to predict the probability of disease presence, survival outcomes, and treatment responses based on patient data. For instance:
- Will a tumor be malignant or benign?
- Will a patient respond to a specific treatment?
Logistic Regression in BioStat Prime: What You Can Do
BioStat Prime does support logistic regression, including binary logistic regression, which is commonly used for modeling binary outcomes such as "yes/no", "success/failure", or "disease/no disease".
Performing Binary Logistic Regression in Biostat Prime
Let's say we want to predict whether a patient has heart disease (1 = Yes, 0 = No) based on two predictors: Age and Cholesterol.
| Patient_ID | Age | Cholesterol | Disease |
|---|---|---|---|
| 1 | 45 | 220 | 1 |
| 2 | 54 | 205 | 0 |
| 3 | 61 | 258 | 1 |
| 4 | 47 | 234 | 0 |
| 5 | 59 | 282 | 1 |
| 6 | 40 | 180 | 0 |
| 7 | 67 | 246 | 1 |
| 8 | 50 | 202 | 0 |
Steps to perform Binary Regression in Biostat Prime
Step 1: Load the Data
- Open BioStat Prime.
- Go to File → Import Dataset and select your CSV file.
- Verify that the columns are correctly recognized.
Step 2: Choose Logistic Regression
- Go to Analysis → Regression → Logistic Regression.
Step 3: Set Up Variables
- Dependent Variable: Select Disease.
- Independent Variables (Predictors): Select Age and Cholesterol.
Step 4: Configure Options
- Choose Binary Logistic Regression.
- Make sure the coding for the binary outcome is correct (usually 0 and 1).
- Enable the display of:
- Coefficients (β)
- Odds Ratios (Exp(β))
- Confidence intervals
- p-values
- Goodness-of-fit statistics (like Cox & Snell R²)
Step 5: Run the Analysis
- Click Run.
- BioStat Prime will output:
- Regression coefficients table
- Odds ratios for each predictor
- Classification accuracy
- ROC curve and AUC if selected
Example Output Interpretation
| Predictor | Coefficient (β) | Exp(β) | p-value |
|---|---|---|---|
| Age | 0.09 | 1.09 | 0.04 |
| Cholesterol | 0.005 | 1.005 | 0.03 |
| Constant | -4.2 | – | 0.01 |
Interpretation:
For every one-year increase in age, the odds of having heart disease increase by 9%.
For every unit increase in cholesterol, the odds increase by 1.5%.
Both predictors are statistically significant (p < 0.05).
Advantages of Binary Logistic Regression
- Interpretability: The model is easy to understand and explain, especially through odds ratios.
- Handles Non-linear Relationships: It doesn’t assume a linear relationship between predictors and the outcome.
- Clarity with Small Datasets: Unlike many regression models, logistic regression performs well even with small (or moderately sized) datasets.
- Probabilistic Output: It gives you probabilities, which are useful for decision-making under uncertainty.
Limitations of Binary Logistic Regression to Keep in Mind
- Assumes Linearity in Log-Odds: While more flexible than linear regression, it still assumes a linear relationship between predictors and the log-odds of the response.
- Sensitive to Outliers: Outliers in predictors can affect the model performance.
- Limited to Binary Outcomes: Multinomial logistic regression is needed for more than two categories.
- Multicollinearity Issues: Highly correlated predictors can distort coefficient estimates and reduce interpretability.
Conclusion
Binary logistic regression is a cornerstone of predictive analytics when the outcome is categorical and binary. It strikes a balance between simplicity and effectiveness, offering a robust framework for modeling probabilities, understanding influencing factors, and making data-driven decisions.
Biostat Prime, our Biostatistical software, will help you get started with statistical modeling and logistic regression. It is simple to implement, yet rich in insight.