In statistical analysis especially in biomedical, pharmaceutical, public health, and life-science research researchers often face a common question:
Should I use ANOVA or Regression for my analysis?
Both techniques are fundamental tools in modern data analysis. They come from the same general linear model family and often lead to similar interpretations. However, they serve different purposes, answer different scientific questions, and provide different capabilities. Choosing the wrong method may oversimplify your results, reduce statistical power, or limit your ability to understand meaningful biological relationships.
With the rise of advanced biostatistical software like BioStat Prime, researchers can now explore these techniques more intuitively and visually. Understanding when to choose one method over the other can significantly enhance your analytical workflow, improve the quality of your scientific conclusions, and streamline the decision-making process in research and development.
Understanding ANOVA vs regression is essential for designing robust analyses, maximizing statistical power, and avoiding misleading results in BioStat Prime.
What Is ANOVA?
ANOVA (Analysis of Variance) is a statistical method used to compare the means of three or more groups. It helps determine whether the observed differences among group means are statistically significant or simply due to random variation.
ANOVA is especially useful when you have categorical predictors such as treatment groups, dose groups (low, medium, high), or clinical categories (mild, moderate, severe).
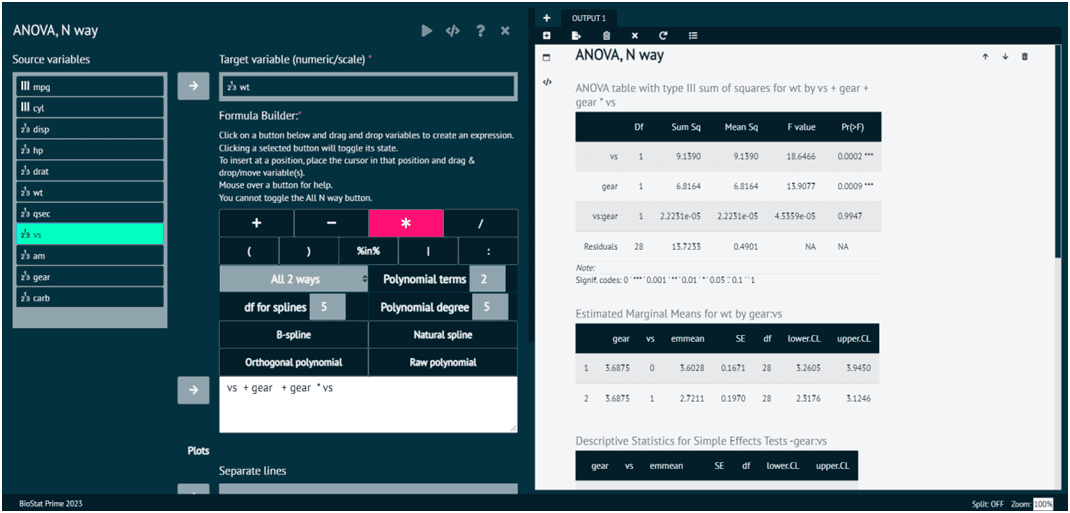
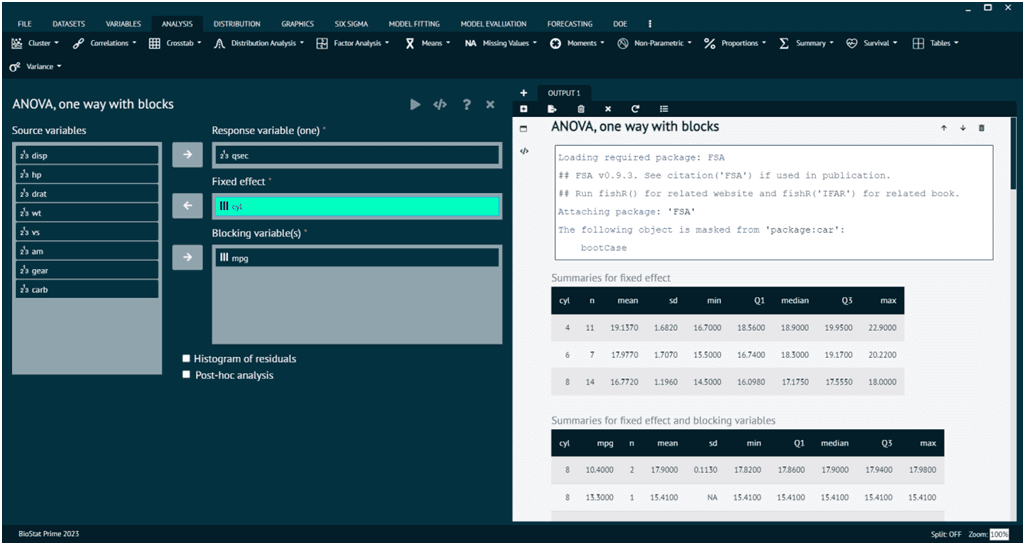
When Is ANOVA Typically Used?
ANOVA is the preferred method when the main scientific objective is to compare group means defined by categorical factors. In biostatistics and experimental biology, typical ANOVA use-cases include:
- Comparing experimental groups
- Comparing treatments or conditions
- Comparing methods, machines, or batches
- Clinical trial arms comparison
- Dose-response comparisons (categorical doses)
- Grouping patients based on risk categories
In all these situations, ANOVA vs regression comes down to whether predictors are truly categorical and whether the goal is primarily to detect any mean differences across groups rather than build a full predictive model.
Types Of ANOVA:
Several ANOVA variants are widely used in biomedical statistics, all of which are supported or easily configured in BioStat Prime.
1. One-Way ANOVA:
Compares means of groups defined by one categorical variable.
Example: Comparing mean systolic blood pressure across three antihypertensive drugs.
2. Two-Way ANOVA:
Compares means based on two categorical variables; evaluates main effects and interaction effects.
Example: Testing whether treatment effect differs between males and females.
3. Repeated Measures ANOVA:
Used when measurements are taken repeatedly on the same subjects.
Example: Monitoring a biomarker before treatment, mid-treatment, and after treatment for the same patient.
What ANOVA Cannot Do:
While ANOVA is highly effective for comparing categorical groups, it carries several limitations that become critical when working with complex, real-world biomedical datasets:
- ANOVA cannot model continuous predictors (e.g., age, dose, time).
- It cannot provide a predictive equation.
- It cannot evaluate linear or nonlinear relationships.
- It cannot handle moderation/mediation.
- It cannot easily incorporate covariates unless extended to ANCOVA.
These limitations are exactly why regression models often outperform ANOVA in complex biomedical and life-science research workflows.
What Is Regression?
Regression analysis comprises statistical methods that quantify how a dependent variable responds to variations in one or more independent variables. Unlike ANOVA, regression accommodates both continuous and categorical predictors and extends naturally to specialized models for binary, count, survival, and nonlinear outcomes.
Regression is a predictive modeling technique that evaluates the relationship between:
- One dependent (outcome) variable
- One or multiple independent predictor variables
Predictors can be:
- Continuous
- Categorical
- Binary
- Mixed
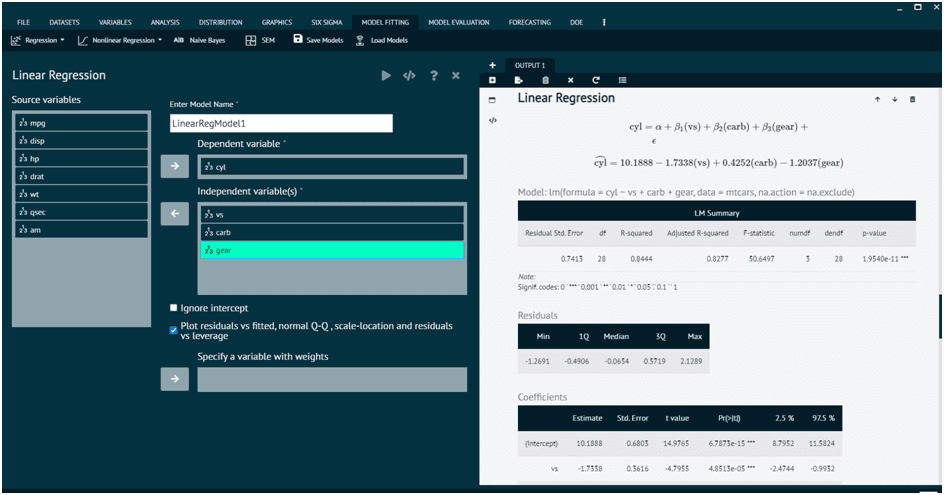
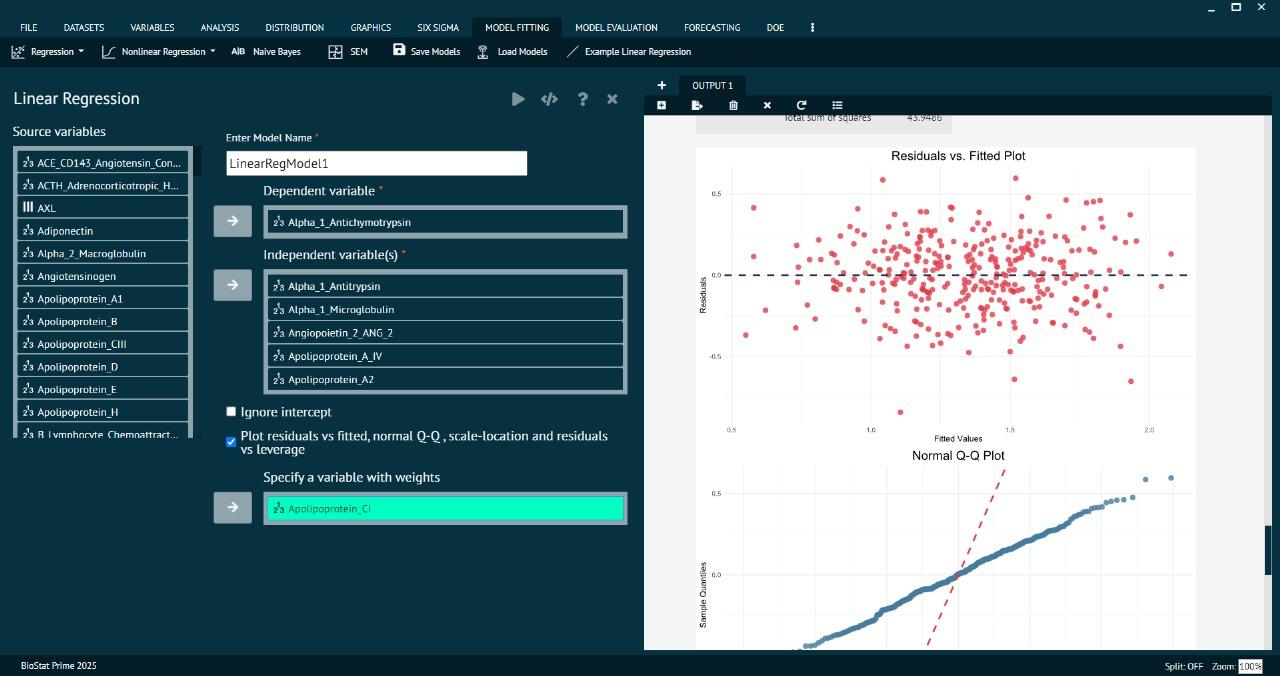
Types Of Regression Commonly Used In Biosciences
BioStat Prime supports a broad range of regression models, covering the main needs of biomedical and public health research.
- Linear Regression
- Multiple Linear Regression
- Logistic Regression
- Poisson Regression
- Nonlinear Regression
- Polynomial Regression
- Hierarchical / Mixed-Effects Regression
What Can Regression Do?
The strength of regression over ANOVA lies in its ability to model underlying relationships and generate predictions, rather than merely comparing group means:
- Model continuous and categorical predictors
- Predict outcomes
- Quantify relationships (β-coefficients)
- Adjust for covariates
- Model interactions
- Provide predictive equations
- Model curves or nonlinear relationships
- Improve statistical power using continuous variables
Regression offers a broader and more adaptable analytical framework than ANOVA. As a result, it is typically recommended in biostatistical applications that involve continuous predictors, multiple covariates, interaction effects, or scenarios requiring individual-level prediction and interpretability.
How ANOVA & Regression Are Related?
Many researchers are surprised to learn that ANOVA is actually a special case of regression.
- ANOVA models categorical groups as dummy variables in a regression equation.
- Both use:
- Sums of squares
- F-tests
- p-values
- R²
- Residual analysis
- Both assume linear relationships (unless nonlinear models are used).
However, regression allows:
- More predictors
- Variable types beyond categories
- Interaction terms
- Customized models
This is why many modern workflows, especially in biostatistics, prefer regression.
When to Use Regression Instead of ANOVA
In biostatistical practice, numerous analytical contexts demonstrate the clear superiority of regression over ANOVA, establishing it as the default framework for rigorous, data-driven inference.
When Your Predictor Is Continuous
Use regression when the independent variable is continuous.
Examples:
- Dose in mg/kg
- Age in years
- Time in hours
- Gene expression levels
- Biomarker concentrations
- Enzyme activity
Reason:
- ANOVA requires grouping continuous variables (which reduces power).
- Regression uses the original continuous scale, providing more precise analysis.
Example:
Instead of categorizing age into "young, adult, old," regression allows you to model age as a continuous predictor.
When You Want a Predictive Equation
ANOVA compares groups but does not provide:
- A prediction model
- A mathematical relationship
- Expected values for new data
Regression provides:
- y = β₀ + β₁x + …
- Prediction intervals
- Ability to forecast outcomes
Useful in:
- Pharmacokinetics
- Clinical prediction models
- Dose-response modeling
- Biomarker-based predictions
When You Have Multiple Predictors
ANOVA handles categorical predictors only.
Regression handles:
- Multiple predictors
- Mixed predictors
- Continuous + categorical variables
If your research question involves controlling for confounding variables, regression is essential.
Example:
Predicting blood glucose using:
- Age
- BMI
- Treatment group
- Lifestyle factors
ANOVA cannot do this effectively.
When You Need to Adjust for Covariates?
ANOVA ignores potential confounders unless converted to ANCOVA.
Regression includes covariates naturally.
Example:
Analyzing drug effect while adjusting for:
- Baseline measurements
- Gender
- Weight
- Disease severity
Regression handles all these simultaneously.
When You Need Interaction Terms
Both ANOVA and regression allow interactions, but regression offers more flexibility.
Example:
Does age modify the effect of treatment?
Regression lets you model:
Outcome = Treatment + Age + Treatment × Age
This is crucial for real-world biomedical models.
When You Want Better Power and Sensitivity
Regression uses continuous variables directly, improving sensitivity.
ANOVA requires grouping continuous variables, which:
- Loses information
- Reduces statistical power
- Increases Type II error risk
Regression is the superior choice in most real datasets.
When Your Outcome Is Not Continuous
ANOVA works only with continuous numeric outcomes.
Regression supports:
- Binary outcomes (Logistic)
- Count outcomes (Poisson)
- Time-to-event outcomes (Cox)
- Rates and proportions
Example:
Predicting disease presence (yes/no).
Only regression can handle this.
When You Need Curve Fitting or Nonlinear Models
ANOVA cannot model curves.
Regression supports:
- Polynomial relationships
- Exponential models
- Sigmoidal dose-response models
- Michaelis-Menten kinetics
Essential in:
- Enzyme kinetics
- Pharmacodynamics
- Growth curves
- Calibration curves
Practical Examples for BioStat Prime Users
Scenario 1: Dose vs. Response
- If dose is categorical → ANOVA
- If dose is continuous → Regression
Regression is preferred because the dose is naturally continuous.
In practice, many biostatisticians prefer regression for dose-response modeling even if data are collected at discrete levels when dose is conceptually continuous.
Scenario 2: Clinical Trial with Baseline Adjustment
You want to compare post-treatment biomarker levels while adjusting for baseline value.
- ANOVA → Cannot adjust
- Regression → Can include baseline as covariate
Therefore: Use regression.
Scenario 3: Predicting Blood Pressure
Predict SBP using:
- Age (continuous)
- Sex (categorical)
- BMI (continuous)
- Treatment (categorical)
Only regression can analyze all variables together.
Scenario 4: Modeling Enzyme Kinetics
Michaelis-Menten cannot be done using ANOVA.
Regression (nonlinear) is the correct tool.
Scenario 5: Gene Expression as Predictor
Gene expression is continuous.
Use regression rather than ANOVA.
How BioStat Prime Simplifies ANOVA And Regression?
BioStat Prime is designed as a biostatistics and graphing software that makes both ANOVA and regression accessible without coding.
- Dedicated One-Way, Two-Way, and Repeated Measures ANOVA modules
- Fully featured Linear and Multiple Regression
- Logistic, Poisson, and Nonlinear Regression
- Easy model selection
- Automatic assumption checks
- Visual plots:
- Residual plots
- QQ plots
- Fit curves
- Interaction plots
- Scatter with regression lines
- Model comparison charts
- Smart data handling
- Exportable reports
BioStat Prime also offers context-based recommendations, helping beginners choose the right test based on their data type and research question.
Common Mistakes In Choosing ANOVA Vs Regression
Researchers frequently make predictable errors when deciding between regression and ANOVA.
- Mistake 1: Converting continuous predictors to categories just to use ANOVA - This reduces statistical power and may bias estimates, especially with arbitrary cut-points.
- Mistake 2: Using ANOVA with non-normal or non-continuous outcomes - When outcomes are binary or counts, appropriate regression models (logistic, Poisson, etc.) should be used instead.
- Mistake 3: Ignoring interactions - Many clinical effects vary by age, sex, or baseline risk; regression models handle interaction terms naturally but are often under-used.
- Mistake 4: Not adjusting for covariates - Simple ANOVA can oversimplify complex biomedical data, leading to confounded results that regression could correct.
- Mistake 5: Treating ANOVA and regression as unrelated tools - In reality, ANOVA is just regression with categorical predictors; thinking of them in one unified framework clarifies model choice.
Summary Table: When to Use Regression Instead of ANOVA
Below is a clear comparison of when regression is preferred over ANOVA.
| Categorical predictors | Yes | Yes |
| Continuous predictors | No | Yes |
| Multiple predictors | Limited | Yes |
| Covariate adjustment | Limited/ANCOVA | Yes |
| Predictive modeling | No | Yes |
| Nonlinear relationships | No | Yes |
| Binary / count outcomes | No | Yes |
| Statistical power for trends | Moderate | High |
| Interaction effects | Yes | Yes |
ANOVA in Regression (Analysis of Variance in Regression)
ANOVA in regression is used to evaluate how well a regression model explains variability in the dependent variable. While ANOVA traditionally compares group means, in regression it partitions the total variability in the outcome into components explained by the model and by random error.
Why ANOVA Is Used in Regression
ANOVA helps answer the question:
"Does my regression model explain a significant amount of variation in the outcome?"
It provides:
- Model significance
- F-test for overall regression
- Breakdown of variability (SS, MS, F, p-value)
- Comparison between explained vs. unexplained variability
The ANOVA Table in Regression
A typical regression ANOVA table contains:
| Source of Variation | Sum of Squares (SS) | Degrees of Freedom (df) | Mean Square (MS) | F-value | p-value |
|---|---|---|---|---|---|
| Regression | SSR | p | MSR = SSR/p | F = MSR/MSE | — |
| Residual (Error) | SSE | n - p - 1 | MSE = SSE/(n-p-1) | — | — |
| Total | SST | n - 1 | — | — | — |
Where:
- SST = Total variability in Y
- SSR = Variability explained by the model
- SSE = Variability not explained (error)
- p = number of predictors
- F-value tests whether the regression model significantly reduces error compared to no model
Key Interpretation
1. F-Test (Overall Model Test)
- H₀: All regression coefficients = 0
- H₁: At least one predictor contributes
If p < 0.05, the regression model is statistically significant.
Connection Between ANOVA and R²
R² = SSR / SST
Higher SSR means more variance explained and thus a higher R². ANOVA provides the numerical foundation for calculating and interpreting R².
Why This Matters in Biostatistics
ANOVA in regression is widely used in:
- Dose-response modeling
- Clinical outcome prediction
- Biomarker-disease association studies
- Epidemiological trend analysis
- Public health risk modeling
It provides a global test before interpreting individual coefficients.
Advantages of Using ANOVA in Regression
- Separates explained vs. unexplained variance
- Validates whether a linear model is useful
- Helps compare nested models
- Supports Type I, II, and III ANOVA tests in complex designs
Traditional ANOVA vs. Regression ANOVA
| Traditional ANOVA | ANOVA in Regression |
|---|---|
| Compares means across categories | Evaluates regression model fit |
| Uses only categorical predictors | Allows continuous and categorical predictors |
| Tests group differences | Tests explained variance |
| Single F-test | F-test for full model |
Short Biostatistics Example
Predicting systolic blood pressure (SBP) using age, BMI, and cholesterol: ANOVA in regression will tell you whether the model predicts SBP significantly, how much variance is explained (R²), and whether the regression model is better than using mean SBP alone
FAQ
Not exactly. ANOVA is a special case of regression where all predictors are categorical.
Yes. Regression will automatically convert categories into dummy (0/1) variables.
Avoid this unless scientifically justified; you lose information and reduce statistical power.
Yes. Polynomial regression and nonlinear regression methods can model curved relationships such as sigmoidal dose–response or Michaelis–Menten kinetics.
Use logistic regression, which is specifically designed for binary outcomes and provides odds ratios and predicted probabilities.
Regression is the better choice because it offers both interpretation and prediction.
Yes. BioStat Prime provides one-way, two-way, and repeated-measures ANOVA as well as linear, multiple, logistic, Poisson, and nonlinear regression.
ANCOVA is essentially regression with both categorical and continuous variables.
ANOVA is simpler conceptually, but BioStat Prime makes regression equally accessible with guided workflows.
Consider three things: outcome type (continuous vs. binary vs. count), predictor type (categorical vs. continuous), and your goal (group comparison vs. prediction/modeling). For continuous predictors, multiple covariates, or predictive modeling, regression is usually the best choice.
Conclusion
ANOVA remains a valuable tool, especially when comparing categorical groups. However, regression is more flexible, powerful, and suitable for real-world biomedical and life-science datasets.
Thinking of ANOVA vs regression as two views of the same general linear model and using regression whenever your data support it, helps you extract more information, reduce bias, and increase statistical power.
You should choose regression instead of ANOVA when:
- Your predictor is continuous
- You need to adjust for covariates
- You want predictions
- You have multiple predictors
- Your outcome is not continuous
- You need nonlinear modeling
- You want maximum statistical power
BioStat Prime is designed to support both methods with an intuitive interface, making it easier for researchers to select the correct model and interpret results accurately.